Temporally characterizing ultrashort laser pulses (on the femtosecond scale, i.e., 10-15 seconds) is akin to reconstructing a crime scene: the light pulses are so fast that we can’t catch them in the act, we can only reconstruct them from the clues they leave behind.
Typically, we work with linearly polarized scalar pulses, in which the polarization state remains constant over time (polarization refers to the trajectory described by the light in the transverse plane). To identify these pulses, we need to know their amplitude or intensity and their phase. There is another type of pulses in which polarization varies over time, known as vector pulses. These are more complex than scalar pulses, and we need to know the amplitude and phase of their two components, as well as the relative phase between them. If identifying a scalar pulse is equivalent to identifying a criminal, knowing a vector pulse would be like knowing a gang composed of two criminals, and moreover, the relationship between them.
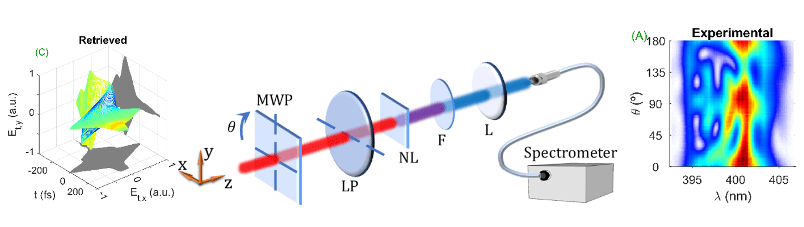
One type of characterization techniques is based on measuring the spectrum of a nonlinear signal while the pulse undergoes some modification. In the amplitude swing technique (a-swing), developed by researchers from the ALF group, two replicas of the pulse to be measured are generated, temporally delayed from each other, and the second harmonic spectrum (frequency doubling) is measured for different relative amplitudes of these replicas. Thus, a two-dimensional trace is obtained (a map where color represents intensity), which is like a fingerprint of the pulse. In some techniques, ambiguities arise, i.e., two different pulses generate the same trace, as if two people had the same fingerprint. Through algorithms, the information of the pulse generating the trace (our clue) can be extracted.
Most techniques only allow the characterization of scalar pulses. If we want to reconstruct a vector pulse with one of these techniques, we need several traces, i.e., several fingerprints. In contrast, a single a-swing trace contains the necessary information to identify a vector pulse. Furthermore, these traces are obtained with an inline, compact, and versatile setup.
In this work, we analyze the a-swing traces analytically and numerically to study how the information of vector pulses is encoded, and we develop a strategy to extract it. This strategy is applied to simulated and experimental traces, demonstrating that a vector pulse can be reconstructed from its a-swing trace. If they don’t want to be caught, they’ll have to avoid leaving these kind of fingerprints…
More information at:
Cristian Barbero, Benjamín Alonso, and Íñigo J. Sola, “Characterization of ultrashort vector pulses from a single amplitude swing measurement,” Opt. Express 32, 10862-10873 (2024) https://doi.org/10.1364/OE.515198

Leave a Reply